Формулы сокращенного умножения
Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 - 2 • 3,16 • 1,16 + 1,162. Если вы начнете считать это "в лоб", получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!
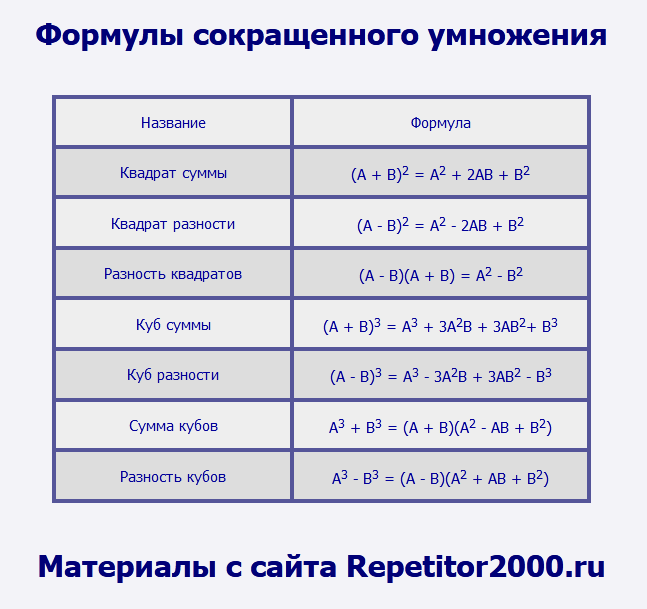
Итак, семь формул "школьной" алгебры, которые должны знать все:
| Название | Формула |
| Квадрат суммы | (A + B)2 = A2 + 2AB + B2 |
| Квадрат разности | (A - B)2 = A2 - 2AB + B2 |
| Разность квадратов | (A - B)(A + B) = A2 - B2 |
| Куб суммы | (A + B)3 = A3 + 3A2B + 3AB2+ B3 |
| Куб разности | (A - B)3 = A3 - 3A2B + 3AB2 - B3 |
| Сумма кубов | A3 + B3 = (A + B)(A2 - AB + B2) |
| Разность кубов | A3 - B3 = (A - B)(A2 + AB + B2) |
Версия для печати в формате png
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы - на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n - произвольное натуральное число? Можно ли увидеть здесь какую - либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)n = An + Cn1An-1B + Cn2An-2B2 + ... + CnkAn-kBk + ... + Bn.
Здесь Cnk = n!/(k! • (n-k)!).
Напоминаю, что n! - это 1 • 2 • ... • n - произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An - Bn?
Да, можно. Вот эта формула:
An - Bn = (A - В)(An-1 + An-2B + An-3B2 + ... + Bn-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
An + Bn = (A + В)(An-1 - An-2B + An-3B2 - ... + Bn-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.